№1
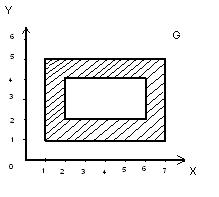
Для определенного графически соответствия G ( рис. 1) определить образы: 1, 3, 6,
[1, 2], [3, 7];
Прообразы: 5, 3, [1, 2], [2, 3].
Каковы свойства соответствия, если:
a) G 
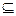N.R б) G 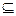N . [1, 5]
№2
Задать такой тип функции f(x)=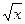 
, чтобы f(x) являлась отображением. Определить вид отображения.
№3
Функции f и g имеют тип f: A3→B, g: B5→C. Найти несколько функций, являющихся композициями f и g, и определить их тип.
№4
Найти композицию преобразований:
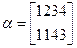
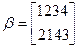
№5
Задать матрицей инцидентности неориентированный граф G1
G1
№6
Задать матрицей смежости ориентированный граф G2. определить локальные степени свободы ρ1(δ) и ρ2(δ)
G2
№7
Построением таблицы истинности подтвердить справедливость правила ((A→B)^A)→B.
№8
Логическую функцию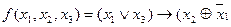 
представить булевой формулой в виде СДНФ
№9
При помощи эквивалентных преобразований доказать: 
