1. Задать различными способами множество натуральных чисел, кратных трем и не превышающих 81.
2. Пусть U={d, e, f, g} определить β(U). Найти его мощность.
3. Пусть U={1, 2, 3, 4, 5, 6, 7, 8}. X={1, 3, 4, 5} Y={1, 5, 6, 7}, Z={3, 4, 6, 7, 8, }. Найти Y∩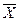 
; (X∩Y) \ (ZUX); 
; 
.
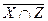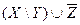4. Доказать при помощи диаграмм Веина справедливость соотношения: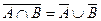 
.
5. Пусть V={(2, 3, 1, 1), (2, 2, 3, 1), (1, 2, 3, 1)}. Найти пр1V, пр2,4V.
6. X={a, c} Y={4, 7}. Найти, X2, X*Y, Y*X*Y.
7. Сравнить векторные оценки множества V. V= {(7, 8, 1, 6), (4, 5, 6,4), (2, 4, 6, 6), (9, 9, 1, 6), (5, 5, 6, 3), (5, 5, 7, 4), (3, 5, 6, 7)}.
8. Составить матрицу отношения, заданного на множестве M={1, 2, 3, 4, 5, 6}, если R означает: “отличаться на 2”. Построить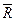 
, R-1, R(2), R0,R*.
9. Каковы свойства отношения “быть сыном”.
10. Пусть на множестве M={1, 2, 3, 4, 5} определено отношение R1-“быть сыном” (рис. 1). Исходя из данных рисунка построить матрицу отношения R1-“быть сыном” и R2-“быть прямым потомком”.
