Графом g называется совокупность двух множеств: вершин V и ребер Е, между элементами которых определенно отношение инцидентности – каждое ребро е 
Е инцидентно двум вершинам ν΄ и ν˝ V, которые оно соединяет. При этом вершины ν΄, ν˝ и ребро е называются инцидентными друг другу, а вершины ν΄ и ν˝, являющиеся для ребра е концевыми точками, называются смежными.
Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой: в этом случае оно называется направленным или ориентированным.
Граф, содержащий направленные ребра (дуги) с началом ν΄ и концом ν˝ называется ориентированным (орграфом), а ненаправленный – неориентированным (н-графом).
Локальной степенью вершины ν V н-графа g называется количество ребер ρ(ν), инцидентных вершине ν. В н-графе сумма степеней всех вершин равна удвоенному числу ребер m графа (петля дает вклад 2 в степень вершины):
Для вершин орграфа определяются две локальные степени:
- ρ1(ν) – число ребер с началом в вершине ν, или количество выходящих из ν ребер;
- ρ2(ν) – количество входящих в ν ребер, для которых эта вершина является концом.
Петля дает вклад 1 в обе эти степени.
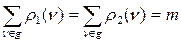, где m – количество ребер для орграфа.
