1. Задать различными способами множество натуральных чисел, кратных 5 и не превышающих 50.
2. Задать различными способами множество М3n (n  N) всех чисел, являющихся степенями тройки и не превышающих 81: 3, 9, ...81.
N) всех чисел, являющихся степенями тройки и не превышающих 81: 3, 9, ...81.
3. Определить в явном виде В(U) и его мощность если:
а) U = {1, 2, 3, 4, 5};
б) U = {а, b, с}.
4. Сколько подмножеств имеет множество, состоящее из трех элементов, из четырех?
5. Проиллюстрировать на конкретном примере некоммутативность операции разности множеств А\В ≠ В\А.
6. Пусть U={1, 2, 3, 4, 5, 6}, А={1, 2, 3}, В={1, 2, 3, 5, 6} , С={4, 5, 6}.
Найти:
а)А\С; б) В\С; в) 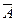 È В ; г)В Ç
È В ; г)В Ç 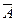 ; д) (С È А)\(С Ç А);
; д) (С È А)\(С Ç А);
е) (СÈ 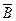 ) Ç А; ж)(А\
) Ç А; ж)(А\ 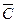 )È(B\
)È(B\ 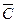 )
)
7. Пусть U={а, b, с, d}, X={а, с}, Y={а, b, d}, Z={b, с}.
Найти множества:
а) 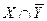 ; б)
; б) 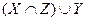 ; в)
; в) 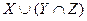 ; г)
; г) 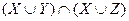 ;
;
д) 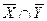 ; е)
; е) 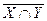 ; ж)
; ж) 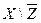 ; з)
; з) 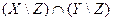 .
.
8. Проиллюстрировать на примере конкретных множеств и с помощью диаграмм Венна справедливость следующих соотношений:
а) 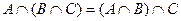 ;
;
б) 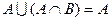 ;
;
в) 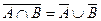 ;
;
г) 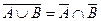 ;
;
д) 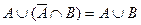 .
.
9.Построить диаграммы Венна, иллюстрирующие множества а) - з) из упражнения 7.