Определитель матрицы n-го порядка равен сумме произведений элементов любой строки (столбца) матрицы на соответствующие им алгебраические дополнения.
Этот способ вычисления определителя называется разложением определителя по элементам некоторой строки (столбца) или разложением Лапласа.
При этом схемы разложений определителя по выбранной строке или выбранному столбцу будут выглядеть соответственно:
 ;
;
 -
-
Пример.
Вычислим определитель третьего порядка, разложив его по элементам первой строки:

 =
= 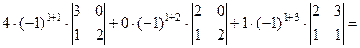
 .
.