 ,
,


 .
.
Данную формулу можно не запоминать, а применять по схематическому правилу треугольников.














 .
.
Пример.

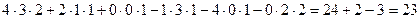 .
.
Для того чтобы обобщить методику вычисления определителей квадратных матриц, введем понятие минора и алгебраического дополнения.
Определение 1.8 Минором 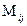 выбранного элемента
выбранного элемента  матрицы n-го порядка называется определитель (п–1)-го порядка, полученный из исходной матрицы путем вычеркивания в ней строки и столбца, на пересечении которых находится этот элемент.
матрицы n-го порядка называется определитель (п–1)-го порядка, полученный из исходной матрицы путем вычеркивания в ней строки и столбца, на пересечении которых находится этот элемент.
Например, если исходной матрицей является матрица 3-го порядка
 , то
, то  а
а  .
.
Определение 1.9 Алгебраическим дополнением  элемента
элемента  квадратной матрицы называется ее минор, взятый со знаком плюс, если сумма индексов выбранного элемента
квадратной матрицы называется ее минор, взятый со знаком плюс, если сумма индексов выбранного элемента  – четное число, и со знаком минус, если эта сумма нечетная, т. е.
– четное число, и со знаком минус, если эта сумма нечетная, т. е. 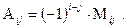
Рассмотрим матрицу n-го порядка 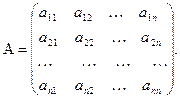
Пример. Дана матрица  .
.
1) Найдем минор и алгебраическое дополнение к элементу  .
.


 = 1;
= 1;  =
= 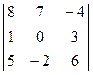 =
= 
 = 42 – (-4)(-2) = 34 ;
= 42 – (-4)(-2) = 34 ;
 = (-1) 2+1
= (-1) 2+1  = -
= -  = - 34.
= - 34.
2) Найдем минор и алгебраическое дополнение к элементу  .
.
 =6;
=6; 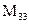 =
= 
 = 0 –7 = -7;
= 0 –7 = -7;  = (-1) 3+3 (-7)= - 7.
= (-1) 3+3 (-7)= - 7.
Рассмотрим матрицу n-го порядка  и введем общее правило подсчета определителя n-го порядка.
и введем общее правило подсчета определителя n-го порядка.