Пусть A, B, C – матрицы, a и β – действительные числа.
1) Коммутативность сложения
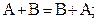
| 5) 
|
2) Ассоциативность сложения
| 6) 
|
3) Дистрибутивность относительно суммы матриц
| 7) 
|
4) Дистрибутивность относительно суммы чисел
| 8) 
|
Определение 1.6 Произведением двух матриц, первая из которых имеет размер 
, а вторая 
называется матрица размером 
, каждый элемент которой, стоящий в позиции 
является суммой произведений элементов 
той строки 1-го сомножителя и соответствующих элементов j-того столбца 2-го множителя. (Правило: строка на столбец).
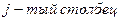
где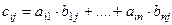 
Пример.
1) 
, 
. 
матрица-столбец
2) 
; 
- умножение невозможно, из-за несоответствия размеров матриц.
3) Найти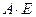 
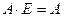
4) Найти и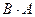 
.
, 
; 
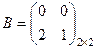
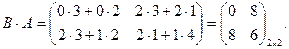
Таким образом, получили, что 
.
Умножение матриц не обладает свойством коммутативности, т.е. в общем случае.
Две матрицы А и В, для которых выполняется равенство 
называются коммутативными.
Легко показать, что 
где А – квадратная матрица, Е – единичная матрица того же размера.
Если для заданных матриц операция умножения определена, то справедливы следующие свойства:
Определение 1.7 Матрица называется транспонированной по отношению к данной, если ее строки являются столбцами данной матрицы, т.е.
, 
.
Пример.
, 
.
2) 
или 
3) 