Для матрицы больших размеров отыскание обратной матрицы удобно проводить с помощью элементарных преобразований над матрицами. Этот метод состоит в следующем. Выписывают составную матрицу 
и по схеме метода Гаусса выполняют над строками этой матрицы (т.е. одновременно и в матрице А и в матрице Е) элементарные преобразования. В результате матрица А преобразуется в единичную матрицу, а матрица Е – в матрицу 
.
Пример. Найти матрицу, обратную к матрице
.
Решение. Запишем составную матрицу и преобразуем ее с помощью элементарных преобразований строк в соответствии с методом Гаусса. В результате получим:
.
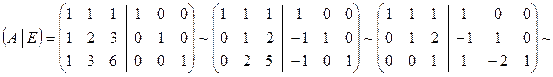
Из этих преобразований заключаем, что
.
