Лекция 6
Произведение двух квадратных матриц n-го порядка всегда определено. При этом важное значение имеет следующая теорема.
Теорема.Определитель матрицы-произведения равен произведению определителей матриц сомножителей: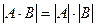 
Доказательство. Пусть
и 
,
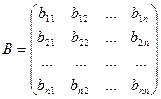тогда
.
Составим вспомогательный определитель
.
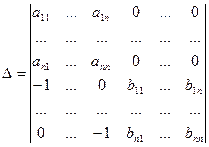По следствию теоремы Лапласа имеем:
.
Итак, 
, покажем, что 
. Для этого преобразуем определитель следующим образом. Сначала первые п столбцов, умноженных соответственно на 
, прибавим к 
-му столбцу. Затем первые п столбцов, умноженных соответственно на 
, прибавим к 
-му столбцу и т.д. На последнем шаге к 
-му столбцу будут прибавлены первые п столбцов, умноженных соответственно на 
. В результате получим определитель
.
Разлагая полученный определитель с помощью теоремы Лапласа по последним п столбцам, находим:
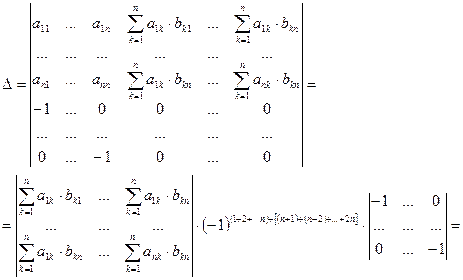
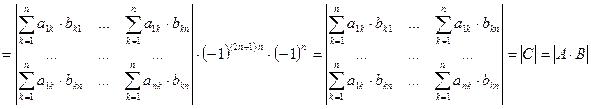
Итак, доказаны равенства и , из которых следует, что .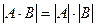
