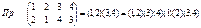Разложение подстановок в произведение независимых циклов.

Def: ] gÎS_n и g=(a₁₁,…,a_1k)(a_S1,…,a_Sks), a_ijiÎ{1,…,n}, причем {a_a1,…,a_aka}Ç{a_b1,…,a_bkb}=Æ, для a,bÎ{1,…,s} и k₁+…+k_s=n, 1£k_i £n. Тогда такое представление подстановки g наз. цикловой записью подстановки g и k_i ~ длине цикла (a_i1…a_ik).

Пр.: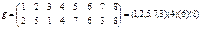

(1,3,5)(2,4)(6)(7)*(1,7,6,)(2,5,4,)(3)=(1,3,2,5,7,6)(4)

Def: 1) подстановка, состоящая из одного не единичного цикла наз. циклом, т.е g=(a₁…a_s); 2) Циклы (a₁,…,a_k) и (b₁,…,b_k)ÎS_n наз. независимыми, если {a₁,…,a_k}Ç{b₁,…,b_k}={Æ}; 3) Подстановки g₁ и g₂ÎS наз. независимыми, если любые циклы подстановок g₁ и g₂ образуют независимые циклы.

Пр.: g₁=(1,2)(3,4), g₂=(5,6,7) Þ g₁ и g₂ – независимые подстановки.

Св-ва: 1) Если g₁ и g₂ – независимые подстановки, то g₁×g₂= g₂×g₁ – композиции; 2) "gÎ S_n представима в виде произведения независимых циклов.