Теорема Кели.

Th Кели: ] G– конечная группа, тогда $ nÎN и $ HÎS_n: G@H ◄] G={g₁,…,g_n}. Рассмотрим j: G®S_n, заданное след. образом

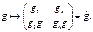
] H=j(G). Покажем, что j– инъективное отображение. Допустим, что g_i^Ù=g_j^Ù, по g_i¹g_jÎG, т.е. g_k×g_i= g_k×g_j(g_k– элементы последней строки подстановки (g_i^Ùg_j) k=1,n Þ g_i=g_j – противореч. Покажем, что j– гомоморфизм, т.е. j(g_ig_j)=g_i^ÙÙg_j =// см. вставку 1//=j(g_i)j(g_j). ] M=j(G), т.о. j: G®j(G)=H является изоморфизмом, т.е G@H<S_G@S_n►

Следствия: 1) Сущ. конечное число различных групп заданного порядка; 2) Число различных конечных групп не более чем счетно.