Утв.: ] G– группа, G1´… ´Gk – внешнее прямое произведение групп G1,…,Gk. Тогда G@G1´… ´Gk Û $ H1,…,Hk<G: 1) Gi@Hi i=1,k; 2)G=H1´·…´·Hk – внутреннее прямое произведение подгрупп H1,…,Hk ◄без док-ва►
Пр.: Z6(+)={0,1,2,3,4,5}, Z3(+)={0,1,2}, Z2(+)={0,1}. Построим внеш. пром. сумму: Z2+·Z3={(a,b): aÎZ2 bÎZ3}.
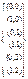
Рассмотрим в Z2+·Z3 мн-во H1={(0,0), (1,0)} – группа, H2={(0,0), (0,1), (0,2)} – группа. Заметим, что H1@Z2(+) {изоморфизм}. j: (*,°)|®*ÎZ2. H2@Z3(+). Рассмотрим Z6(+), рассмотрим подгруппы: <2><Z6 и <2>={0,2,4} (+) – обратный по mod 6, <3><Z6 и <3>={0,3} (+). Покажем, что Z6(+)=<2>+·<3>. Проверим определение: 1) <2>, <3>: <2>DZ6, <3>DZ6 т.к. Z6– аб. группа; 2) <<2>È<3>>=?Z6. Действит.
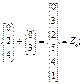
3) <2>Ç<3>={0}. Т.о. Z6@Z2+·Z3.