Определение 1.3. Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом пишут AМB, где Месть знак вложения подмножества. Из определения следует, что для любого множества справедливы, как минимум, два вложения AМA и AМU.
Определение 1.4. Если AМB и A№B и A№Ж, то A называется собственным подмножеством множества B. В этом случае A содержит хотя бы один элемент, не принадлежащий B.
В теории множеств, по определению, полагают, что пустое множество является подмножеством любого множества: Ж№B.
Пустое множество и само множество A называются несобственными подмножествами множества A.
Определение 1.5. Объединением множеств A и B (обозначение AИB) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или В.
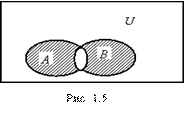
Определение 1.6. Пересечением множеств A и B (обозначение AЗB) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B
Определение 1.7. Разностью A\B множеств A и B называется множество всех тех элементов множества A, которые не принадлежат множеству B
Определение 1.9. Абсолютным дополнением множества называется множество всех элементов, не принадлежащих A, т.е. множество U\A, где U – универсальное множество