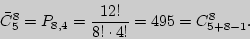В данных выборках допускается повторение элементов, что является достаточно естественным (например, в телефонных и автомобильных номерах возможно использование одной цифры несколько раз).
Число размещений из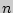 
элементов по 
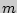с повторениями обозначается 
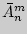и находится как
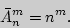
Число перестановок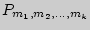 
, в которых 1-й элемент повторяется 
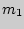раз, 2-й - 
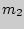раз, а 
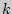-й - 
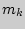раз, находится следующим образом:
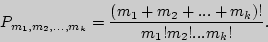
Пример 9.Сколько "слов" можно получить, переставляя буквы в слове МАТЕМАТИКА?
Решение. Заметим, что если бы все буквы были различны, то получили бы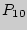 
новых "слов", но буква "М" употребляется в "слове" 2 раза, "А" - 3 раза, "Т" - 2 раза, оставшиеся три буквы - по разу. Следовательно, искомое число будет в 
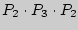раз меньше, чем 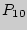, и равно
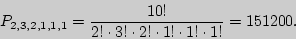
Число сочетаний с повторениями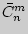 
из 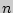элементов по 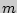выражается через число сочетаний без повторений:
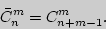
Пример 10. В кафе в продаже имеются 5 сортов пирожных. Сколькими способами 8 студенток могут заказать себе по одному пирожному?
Решение. Зашифруем каждую покупку 8 пирожных единицами по 5 сортам, разделяя сорта нулями. Тогда каждой покупке будет соответствовать упорядоченный набор из 8 единиц и 4 (= 5 - 1) разделительных нулей, а общее число покупок будет соответствовать числу перестановок этих нулей и единиц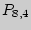 
. Таким образом,
