4. 
1. Запишите матрицы А и В (столбец свободных членов):
1.71 -0.8 1.44 -0.7 1.35
А := 0.64 -0.85 -0.43 0.88 В := 0.7
0.38 1.42 0.63 -1.55 0.28
0.83 -0.6 0.58 -1.22 - 0.47
2. Сформируйте расширенную матрицу, использовав предназначенную для этого функцию: C:=augment(A,B)
1.71 -0.8 1.44 -0.7 1.35
С = 0.64 -0.85 -0.43 0.88 0.7
0.38 1.42 0.63 -1.55 0.28
0.83 -0.6 0.58 -1.22 -0.47
3. Примените метод Гаусса, сформировав единичную матрицу из расширенной, использовав предназначенную для этого функцию: D:= rref(C)
1 0 0 0 1.091
D = 0 1 0 0 0.767
0 0 1 0 0.563
0 0 0 1 1.018
5. 4. Выделите с помощью функции submatrix блок из матрицы D x:=submatrix(D,0,3,4,4) – и вы получите искомый результат (рис. 53):
1.091
X= 0.767
0.563
1.018
где D – название матрицы, из которой находится выделяемый блок,
0 – начальный номер строки выделяемого блока,
3 – конечный номер строки выделяемого блока (нумерация начинается с нуля),
4 – начальный номер столбца выделяемого блока,
4 – конечный номер столбца, выделяемого блока.
5. Выполните анализ всех полученных результатов. И вы увидите, что, решая систему линейных алгебраических уравнений пятью различными способами, вы получили один и тот же ответ, что говорит о правильности найденных результатов.
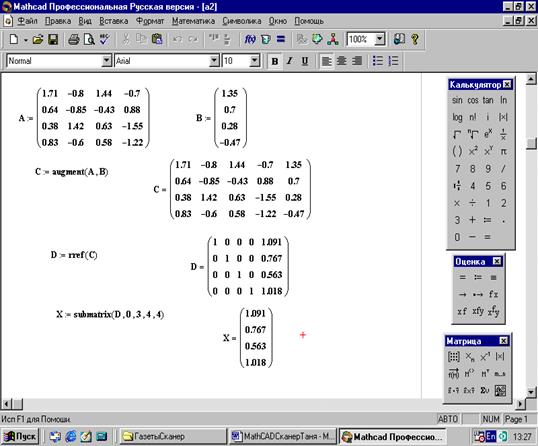
Рис. 53. Решение системы линейных уравнений методом Гаусса
