Задача о коммивояжере обманчива. Ее легко сформулировать, но очень трудно решить. Коммивояжер должен регулярно бывать в каждом из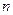 
городов. Между каждой парой городов налажено регулярное воздушное сообщение. Задача состоит в том, чтобы составить такое расписание полетов, чтобы коммивояжер вернулся в тот же город, из которого отправился, побывав при этом ровно по одному разу во всех остальных городах, причем время в пути должно быть наименьшим.
Простейший (и не самый эффективный) алгоритм решения задачи состоит из трех шагов.
Шаг 1: Найти все возможные маршруты.
Шаг 2: Найти время в пути для всех маршрутов, найденных на первом шаге.
Шаг 3: Среди всех маршрутов найти тот, для которого время в пути минимально.
На следующем примере мы проследим за выполнением трех шагов этого алгоритма для множества из четырех городов.
Пример 2.1.1. Для четырех городов даны времена полета из одного города в другой. Найти наилучший маршрут для поездки по этим четырем городам. Число на пересечении 
строки и 
столбца – это время полета из города 
в город 
или из города в город . Ребра соединяют города, между которыми имеется воздушное сообщение. Число возле ребра – продолжительность полета между двумя городами – концам ребра.
