Пусть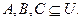 
Каковы бы ни были заданные подмножества 
универсума 
справедливы соотношения:
1. Идемпотентность.
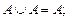
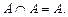
2. Коммутативность.
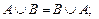
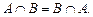
3. Ассоциативность.
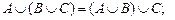
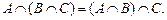
4. Дистрибутивность.
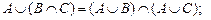
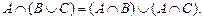
5. Законы поглощения.
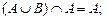
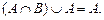
6. Свойства нуля.
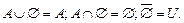
7. Свойства единицы.
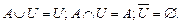
8. Инволютивность.
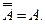
9. Законы де Моргана.
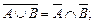
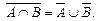
10. 
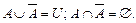
Доказательство этих равенств большей частью совершенно элементарно.
В качестве примера приведем доказательство одного из законов де Моргана.
Утверждение.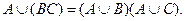 
Доказательство. Пусть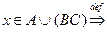 
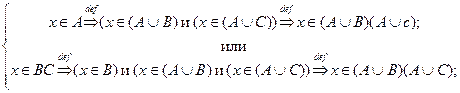
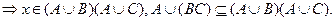
Пусть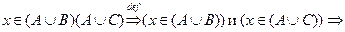 
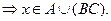
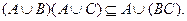
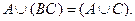
Утверждение.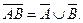 
Доказательство. Пусть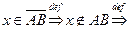 
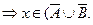
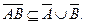
Пусть
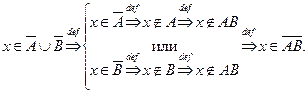
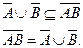
Законы коммутативности и ассоциативности легко распространяются на случай объединения (пересечения) любого конечного числа множеств. Именно, в какой бы последовательности ни объединялись (пересекались) данные множества 
в результате получается одно и то же множество, которое обозначается 
объединение состоит из тех и только тех элементов, которые входят хотя бы в одно из данных множеств (пересечение содержит те и только те элементы, которые входят во все множества одновременно). Запишем обобщение законов дистрибутивности и де Моргана:
;
.
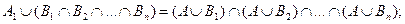
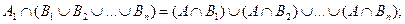
Доказательство проводится, например, методом математической индукции.
