Утверждение, что любое множество однозначно определяется своими элементами, можно сформулировать по-другому.
Определение. (Интуитивный принцип объемности).Два множества 
и 
называются равными, пишется 
тогда и только тогда, когда они состоят из одних и тех же элементов.
Следовательно, если множества и не равны, то существует хотя бы один элемент 
такой, что принадлежит одному из этих множеств, но не принадлежит другому. Пишут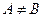 
.
В соответствии с принципом объемности доказательство равенства множеств и нужно проводить в два этапа: доказать, что всякий элемент 
принадлежит также множеству ; доказать, что всякий элемент 
принадлежит и множеству .
Пример 1.2.1. Множество 
равно множеству 
, так как порядок перечисления элементов множества не имеет значения.
Пример 1.2.2. 
, множество слева от знака 
это пустое множество, не содержащее элементов, а множество справа – это множество, содержащее единственный элемент – пустое множество.
Пример 1.2.3. 
так как первое множество – это семейство, содержащее два элемента: множества 
. Второе множество, содержит три элемента – 1, 2, 3.
Пример 1.2.4. Докажем, что множество всех положительных целых четных чисел равно множеству всех положительных чисел, представимых как сумма двух целых положительных нечетных чисел.
