Степеневим рядом називається функціональний ряд
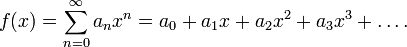
Число 
називають радіусом збіжності степеневого ряду, а проміжок 
- інтервалом збіжності (областю збіжності).Якщо всі коефіцієнти ряду ненульові, то радіус збіжності рівний наступній границі
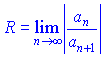
при умові, що вона існує (скінченна чи нескінченна).
Для рядів вигляду
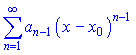
радіус збіжності визначається за формулою 
, проте інтервал збіжності з нерівності
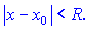
Теорема не дає відповіді про збіжність на кінцях інтервалу, тому їх слід перевіряти окремо за відомими ознаками збіжності.
Розглянемо приклади на знаходження області збіжності степеневого ряду.
Теорема 1 (неперервність суми степеневого ряду). Сума степеневого ряду (13.39) є неперервною всередині проміжку збіжності. Але при члени ряду (13.39) за абсолютною величиною не більші відповідних членів ряду (13.49). Тому, за ознакою Вейєрштрасса, ряд (13.39) рівномірно збігається на відрізку і його сума буде неперервною на цьому відрізку.
Наслідок. Якщо границі інтегрування , лежать всередині інтервалу збіжності степеневого ряду , то за теоремою 3 (п.13.9.3) його можна почленно інтегрувати на проміжку , оскільки він буде рівномірно збігатися на , що містить проміжок
