Ряд
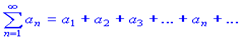
називається знакозмінним, якщо частина його членів приймає додатні значення, а решта - від'ємні.
Знакопочерговим називається ряд, сусідні члени якого мають протилежні знаки. У випадку, коли перший член знакопочергового ряду додатний, його можна подити у вигляді
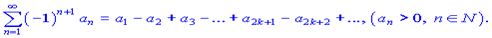
Для дослідження збіжності ряду використовують ознаку Лейбніца: якщо члени знакопочергового ряду спадають по абсолютній величині та
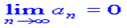
то ряд збіжний. При цьому сума ряду не перевищує значення його першого члена, якщо він додатній.
Для знакозмінного ряду існують поняття абсолютної та відносної збіжності.
Знакозмінний (знакопочережний) ряд збіжний абсолютно, якщо цей ряд та ряд утворений з модулів членів цього ряду збіжні одночасно. Ряд називають умовно або неабсолютно збіжним у випадках, коли збіжний лише знакозмінний ряд, а ряд складений з абсолютних величин членів ряду розбігається.