Ряд вигляду 
називається додатним, якщо всі його члени невід'ємні
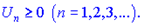
Для того, щоб визначити чи ряд збіжний чи розбіжний в літературі зібрані правила, які дозволяють це швидко. Розглянемо по черзі ознаки збіжності числових рядів.
Ознака порівняння
Розглянемо два ряди з додатними членами 
Гранична ознака порівняння Нехай ряди 
та 
додатні, а також існує скінчена границя
причому 
, тоді обидва ряди або одночасно збіжні, або одночасно розбіжні.
Ознака Даламбера
Нехай члени ряду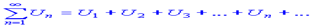 
додатні і відношення 
-го члену до 
-го має скінченну границю при 
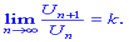
Якщо 
, то ряд збігається.
Якщо 
- ряд розбігається.
При 
треба застосовувати іншу ознаку збіжності, оскільки дана ознака не може визначити чи збіжний ряд чи розбіжний.
Радикальна ознака Коші
Якщо для ряду 
з додатними членами існує границя
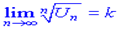
то при ряд збіжний, а при - розбіжний.
При потрібно застосовувати іншу ознаку збіжності.
Інтегральна ознака Коші
Нехай задано ряд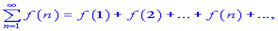 
причому 
додатна, неперервна і монотонно спадна функція від 
.Тоді
1) ряд 
збіжний, якщо невластивий інтеграл
збіжний;
2) ряд розбіжний, коли інтеграл розбіжний.
Під збіжністю інтегралу слід розуміти його обмеженість, тобто
