Метод заміни
При обчисленні визначених інтегралів, як і невизначених, широко користуються методом заміни змінної (або методом підстановки).
Теорема 1. Нехай виконуються умови:
1) функція f(x) неперервна на відрізку [а;b];
2) функція x =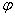 
(t) і її похідна х' = 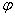(t)' неперервні на відрізку [ 
; 
];
3) 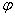(а)=а, 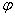( )=b I t 
( ; ):a< 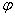(t)<b.
Тоді справджується рівність
Метод інтегрування частинами
Теорема 2. Якщо функції 
i 
мається на відрізку [а;b] мають неперервні похідні, то справедлива формула
(2)
o Оскільки функція uv є первісною функції (uv)' -u'v + uv', то за формулою Ньютона-Лейбніца дістанемо
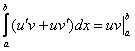
Скориставшись лінійністю визначеного інтеграла, дістанемо формулу (2) 
.
Формула (2) називається формулою інтегрування частинами визначеного інтеграла.
Всі зауваження відносно формули інтегрування частинами невизначеного інтеграла переносяться і на формулу (2).
