Означення: Функція F(x) називається первісною для функції f(x) на проміжку І, якщо на цьому проміжку F'(x) = f(x) або dF(x) = f(x)dx .
Із означення виходить, що первісна F(x) — диференційовна, а значить неперервна функція на проміжку І, і її вигляд суттєво залежить від проміжка, на якому вона розглядається.
Приклад: Первісні для функції  мають вигляд:
мають вигляд:
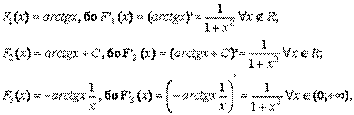
причому, F1(x), F2(x) — неперервні  R, a F3(x) у точці х = 0 має розрив (рис. 7.1). У цьому прикладі первісні Fi(x) і = 1,2,3, знайдені методом добору із наступною перевіркою, використовуючи таблицю похідних функцій.
R, a F3(x) у точці х = 0 має розрив (рис. 7.1). У цьому прикладі первісні Fi(x) і = 1,2,3, знайдені методом добору із наступною перевіркою, використовуючи таблицю похідних функцій.
Нехай функція  неперервна на відрізку [а, b] і відома її первісна
неперервна на відрізку [а, b] і відома її первісна 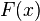 , тоді визначений інтеграл від функції
, тоді визначений інтеграл від функції  можна обчислити за формулою:
можна обчислити за формулою:
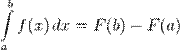
Ця формула називається формулою Ньютона—Лейбніца. Іноді її називають основною формулою інтегрального числення. Для скорочення запису часто застосовується позначення:
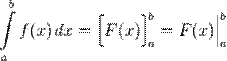
Формула Ньютона-Лейбніца для обчислення визначеного інтегралу є узагальненням методу Архімеда для обчислення площ і поверхонь плоских, криволінійних поверхонь, об'ємів тіл, довжин кривих та інших задач.
Але в багатьох випадках первісна функція не може бути знайдена за допомогою елементарних засобів або є занадто складною, що робить неможливим обчислення визначеного інтеграла за цією формулою. В таких випадках користуються чисельнимим методами обчислення визначених інтегралів.