Рассмотрим сначала ситуацию в общем виде. Пусть A-исходная сумма, S-снимаемая сумма ежегодно, P-процентная ставка.
Тогда через год на счету будет 
, а после снятия денег 
;
Через два года:
, или 
;
Через три года:
, или 
;
Через четыре года:
, или 
и т. д.
Получается, что после снятия в конце года денег на вкладе остается сумма в количестве 
руб
Сумма 
представляет собой конечную геометрическую прогрессию с первым членом 1 и знаменателем 
, а значит, эта сумма равна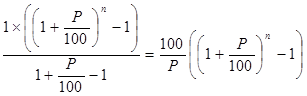 
.
Тогда в итоге получаем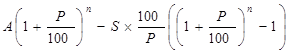 
-закон образования суммы в конце каждого года после съема денег с вклада. В нашем случае получаем:
,
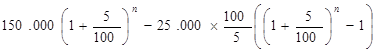и нам необходимо найти, при каком значении n эта сумма станет равной нулю.
;
; 
;
; 
;
; 
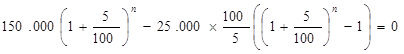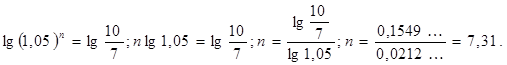
Таким образом, выполнение денежных операций в полном объеме возможно на протяжении 7 лет.
