Весьма часто при проведении психологических исследований требуется установить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Две случайные величины Y и X могут быть связаны либо функциональной зависимостью (Y = f(X) – функция от X), либо статистической зависимостью, либо быть независимыми.
Статистической называют зависимость, при которой каждому значению одной случайной величины соответствует свое распределение другой.
Частным случаем статистической зависимости является корреляционная зависимость, когда изменение одной из случайных величин влечет изменение среднего значения другой.
Сущность корреляционного анализа состоит в отыскании по данным наблюдений вида и параметров функций f(x) и в оценке тесноты связи между величинами X и Y.
Числовой характеристикой тесноты линейной корреляционной связи двух случайных величин служит выборочный коэффициент корреляции:
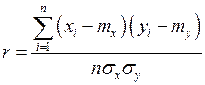
Его значения принадлежат интервалу -1 < r < 1. Чем ближе r к единице, тем связь сильнее, чем ближе r к нулю, тем связь слабее.
Уравнение линии регрессии (в случае линейной корреляционной связи) можно представить в виде:
 .
.
Можно использовать для определения параметров искомой функции методом наименьших квадратов. Такой метод применим и в нелинейных случаях.