Проверка гипотез о характере распределения с помощью критерия 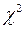 «хи-квадрат» (критерий Пирсона).
«хи-квадрат» (критерий Пирсона).
Пусть имеется m >> n реализаций случайной величины x. Надо проверить гипотезу о том, что функция распределения нормальна. При этом математическое ожидание и дисперсия x оцениваются по выборке. Для проверки этой гипотезы область возможных значений разобьем на n интервалов. Обозначим: pi (i==1, 2,... ,n)– вероятность попасть в i-тый интервал, а mi – число значений в i-том интервале. Тогда величина
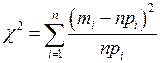
имеет при больших m приближенно 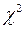 – распределение с n – 3 степенями свободы, т.к. два параметра распределения оценивались статистически. Пользуясь таблицами распределения находят критическое значение
– распределение с n – 3 степенями свободы, т.к. два параметра распределения оценивались статистически. Пользуясь таблицами распределения находят критическое значение  . Если окажется, что вычисленное
. Если окажется, что вычисленное 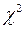 >
>  , проверяемую гипотезу отвергают, а если окажется
, проверяемую гипотезу отвергают, а если окажется 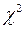 <
<  – принимают.
– принимают.