Пусть количественный признак Х генеральной совокупности распределен нормально со средним квадратичным отклонением s. Тогда с надежностью g можно утверждать, что доверительный интервал
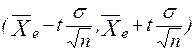
покрывает неизвестное математическое ожидание a.
Здесь  – точность оценки, n – объем выборки. Число t определяется из равенства 2Ф(t) = g. По таблице значений функции Лапласа находят аргумент t, которому соответствует значение функции равное g/2.
– точность оценки, n – объем выборки. Число t определяется из равенства 2Ф(t) = g. По таблице значений функции Лапласа находят аргумент t, которому соответствует значение функции равное g/2.