Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е.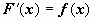 
Свойства первообразной.
- Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x) + C, где C - произвольная постоянная, тоже будет первообразной для f(x) на этом интервале. (Док-во:
). - Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F1(x) может быть представлена в виде F1(x) = F(x) + C, где C - постоянная на X функция.
3. Для любой первообразной F(x) выполняется равенство dF(x) = f(x) dx
Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом 
, где f(x)dx-подынтегральное выражение, f(x)-подынтегральная функция, dx-дифференциал функции.
Свойства неопределенного интеграла: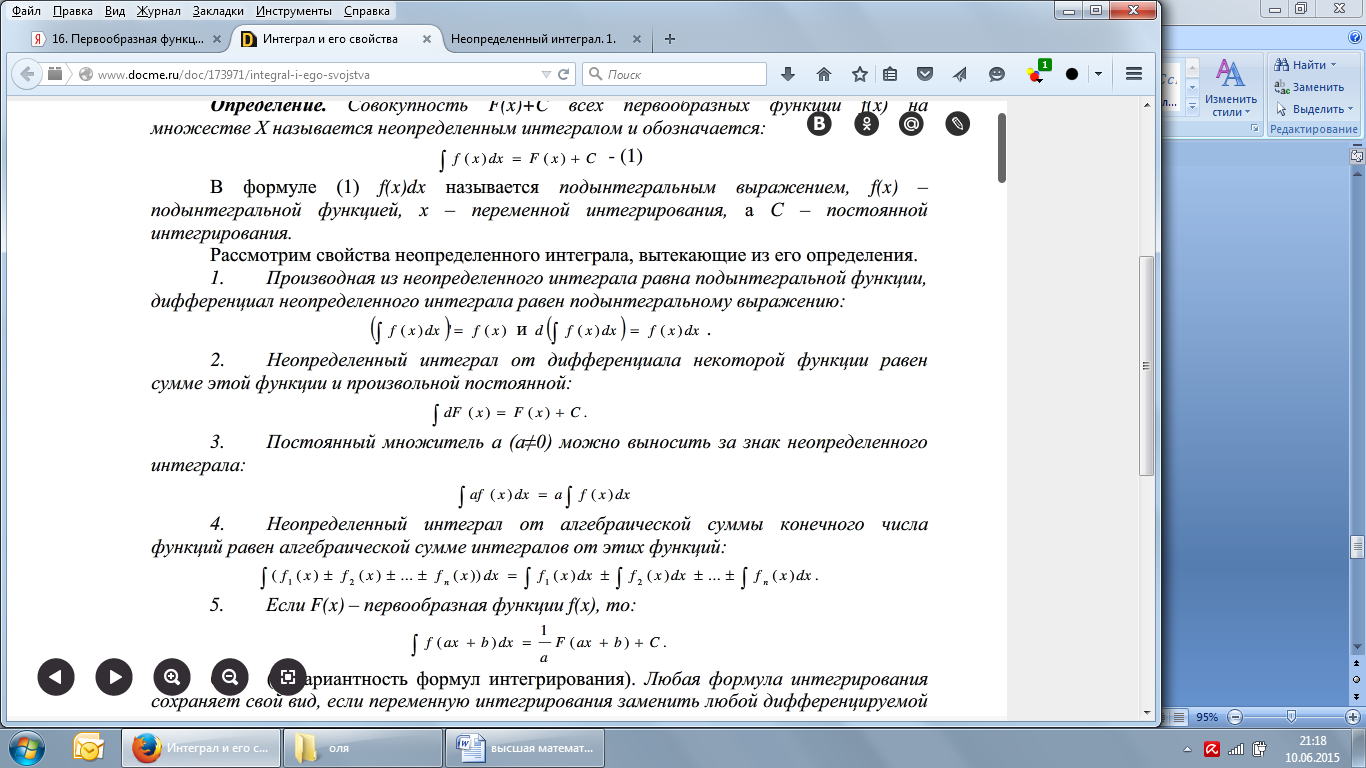 
Интегралы некоторых элементарных функций (таблица интегралов)
Таблица неопределённых интегралов.
| |  .
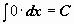| 12.
| . 
|
| |  .
| 13.
| . 
|
| | 
| 14.
| . 
|
| |  .
|
| .
|
| | 
6. 
|
| . 
|
| |  .
|
| 
|
| |  .
| |
| |  .
| |
| |  .
| |
| | 
| |
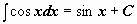