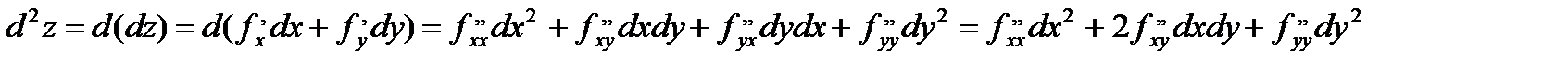Пусть дана функция z=f(x,y). Это функция 2-х переменных х,у. Её частные производные 
и 
также являются функциями 2-х переменных : х и у, т.е. для каждой из них тоже можно найти частные производные:
, 
, 
, 
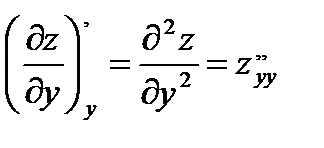
Опр. Производные 
и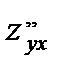 
называются смешанными производными.
Теорема. Если функция z=f(x,y) имеет в некоторой окрестности т М(х,у) смешанные производные 2-го порядка, причем в самой точке эти производные непрерывны, то смешанные производные не зависят от порядка дифференцирования, т.е. =
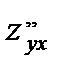
Опр. Пусть дана функция z=f(x,y). Ее дифференциал имеет вид: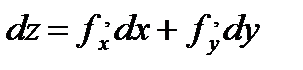 
Тогда дифференциал второго порядка имеет вид:
