Если функция z=f(x,y) дифференцируема, то полный дифференциал dz равен
dz= A∆x+B∆y (1)
Замечая, что 
, 
∆, то уравнение (1) примет вид:
(2)
Распространим понятие дифференциала функции на независимые переменные, положив дифференциалы независимых переменных равными их приращениям ∆x=dx, ∆y=dy. После этого формула полного дифференциала функции примет вид:
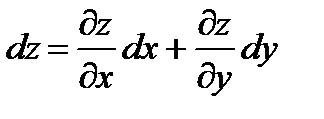
6. Уравнение касательной плоскости к поверхности z=f(x,y), геометрический смысл дифференциала функции 2-х переменных. Использование полного дифференциала в приближенных вычислениях.
Касательной плоскостью к поверхности в ее точке M0 (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.
Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
Если уравнение поверхности имеет вид
F(x,y,z)=0,
то уравнение касательной плоскости в точке M0(x0,y0,z0) есть
F′x(x0,y0,z0)(x−x0)+F′y(x0,y0,z0)(y−y0)+F′z(x0,y0,z0)(z−z0)=0.
В случае задания поверхности в явной форме
z=f(x,y)
уравнение касательной плоскости в точке M0(x0,y0,z0) имеет вид
z−z0=f′x(x0,y0)(x−x0)+f′y(x0,y0)(y−y0),
