Опр. Пусть дана функция z=f(x,y) в некоторой области D пространства R2, проходящая через точку М0(х0,у0)-(внутренняя точка области). Если полное приращение функции в точке М0 можно представить как ∆f=A∆x+B∆y+α(∆d), где ∆х, ∆у - приращение соответственно переменных х и у, а α(∆d) – бесконечно малое расстояние между точками, то функцию z называют дифференциальной в точке М0, а линейная часть этого дифференциала называется полным дифференциалом.
Дифференциал: df= A∆x+B∆y, т.к. ∆x=dx, ∆y=dy, то df= Adx+Bdy.
Теорема (необходимое условие дифференцируемости функции) Если функция z=f(x,y) дифференцируема в точке М0(х0,у0), то в этой точке существуют обе частные производные, причем 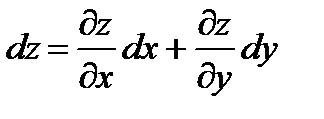
Теорема (достаточное условие дифференцируемости функции) Рассмотрим множество D содержащееся в R2 и произвольную внутреннюю точку М(х,у) принадлежащюю D и дана функция z=f(x,y). Если в некоторой окрестности точки М(окрестность целиком принадлежит D) существуют обе частные производные, а в самой точке эти производные непрерывны, то данная функция дифференцируема в заданной точке М.