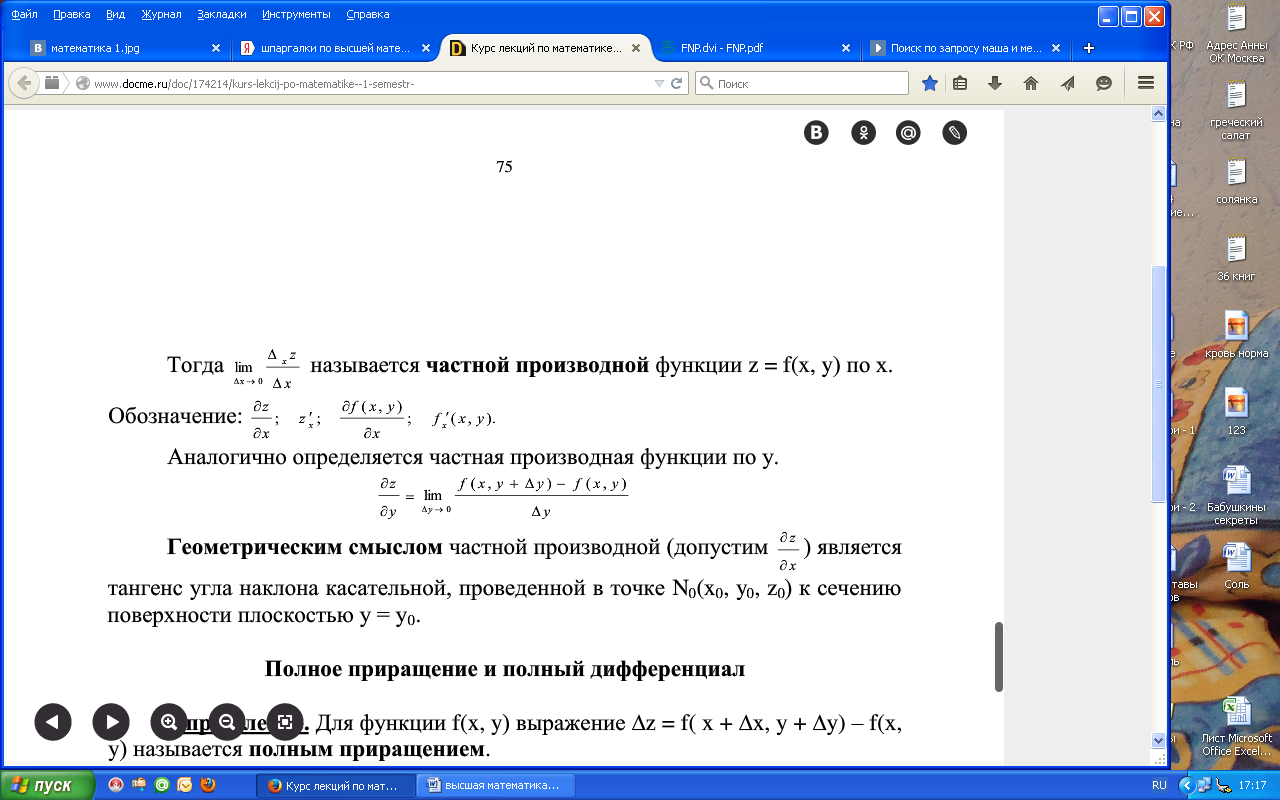
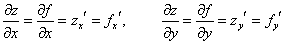Опр. Пусть в некоторой области задана функция z=f(x,y). Возьмем произвольную точку М(х,у) и зададим приращение ∆х к переменной х. тогда величина ∆хz=f(x+∆x,y)-f(x,y) называется частным приращением функции по переменной х, т.е. 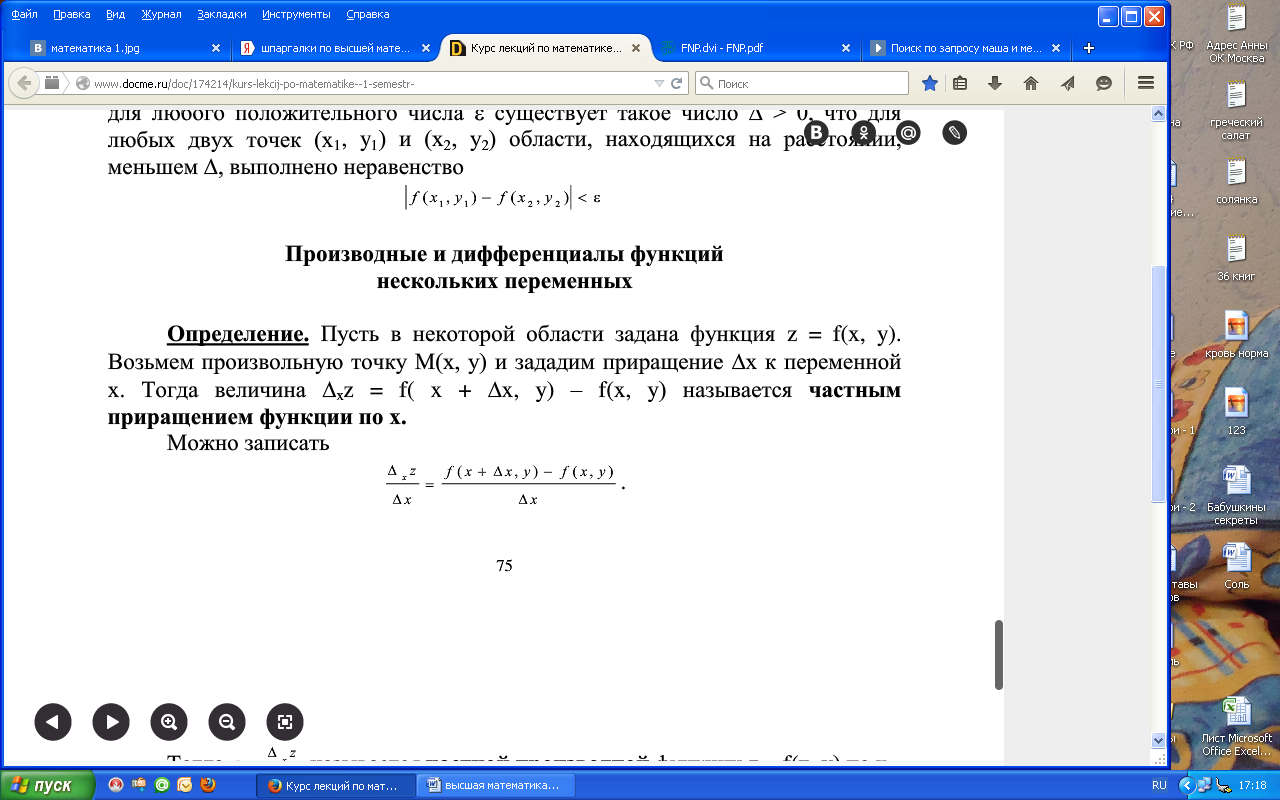
Опр. Если существует предел отношения частного приращения функции по переменной х к приращению аргумента ∆х, при ∆х→0, то говорят, что данный предел есть частная производная функции по переменной х.
Для функций нескольких переменных вводится понятие частной производной первого порядка, то есть производной функции по одной из переменной при условии, что остальные переменные фиксированы. Например, для функции двух переменных z = f(x, y) рассматриваются частные производные по переменной x и по переменной y. Они обозначаются следующим образом: