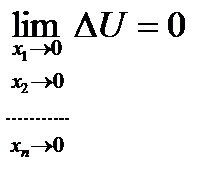Пусть в n-мерном пространстве Rn на множестве Е задана функция U=f(M), где M(x1,x2,…,xn). Пусть точка М*(x*1,x*2,…,x*n) является предельной точкой данного множества.
Опр. (по Коши) Число А называется пределом функции U=f(M) в точке М* если для любого ε>0 найдется такое число δ, что для всех точек М удовлетворяющих неравенству d(M,M*)<δ выполняется Іf(M)-AІ< ε, т.е.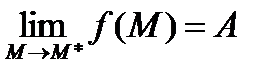 
Опр. (по Гейне) Число А называется пределом функции U=f(M) в точке М* если для любой последовательности {Мк} содержащейся во множестве Е такой что точки Мк стремятся к М* соответсвующая последовательность значений функции f(Mk) устремится к А.
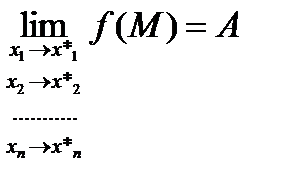
Предел функции в точке по Коши и по Гейне эквивалентны.
Опр. Пусть на множестве D содержащемся в n-мерном пространстве Rn задана функция f(x1,x2,…,xn) имеющая предельную точку М0(x 
1,x 
2,…,x n). Функция называется непрерывной в точке М0 если предел функции в данной точке равен значению функции в точке М0, т.е.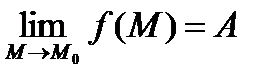 
Опр. Функция f(M) называется непрерывной в точке М0 если предел полного приращения функции равен 0, только в случае, когда приращение по всем переменным стремится к 0, т.е. 
