Уравнение вида: 
где j и Ψ - известные функции от 
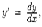называется урaвнeниeм Лагранжа. Введем вспомогательный параметр, положив у'=р. Тогда уравнение (1) примет вид 
Дифференцируя по х, получим: 
т. е. 
или 
Уравнение (3) есть линейное уравнение относительно неизвестной функции х= х(р). Решив его, найдем: 
Исключая параметр р из уравнений (2) и (4), получаем общий интеграл уравнения (2.25) в виде у=γ(х;с). Отметим, что, переходя к уравнению (3), мы делили на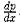 
При этом могли быть потеряны решения, для которых 
т. е. р=ро=const.Это значение ро является корнем уравнения р-j(р)=0 (см. (2.27)). Решение 
является особым для уравнения (2.25)
