Бернулли – это уравнение вида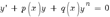 
Решение дифференциального уравнения Бернулли приведением к линейному уравнению Исходное уравнение:
(1)
Разделим на yn. При y ≠ 0 имеем
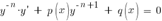
Это уравнение сводится к линейному с помощью замены переменной:
По правилу дифференцирования сложной функции
Подставляем:
Или:
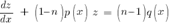
49 Уравнения в полных дифференциалах
Дифференциальное уравнение вида
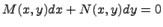
называется дифференциальным уравнением в полных диффернциалах, если его левая часть является полным дифференциалом некоторой гладкой функции 
, т.е. если 
, 
. Необходимое и достаточное условие для существования такой функции имеет вид:
Чтобы решить дифференциальное уравнение в полных дифференциалах необходимо найти функцию 
. Тогда общее решение дифференциального уравнения можно записать в виде 
для произвольной постоянной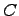 
.
Интегрирующим множителем для дифференциального уравнения
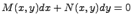
называется такая функция 
, после умножения на которую дифференциальное уравнение превращается в уравнение в полных дифференциалах. Если функции 
и 
в уравнении имеют непрерывные частные производные и не обращаются в ноль одновременно, то интегрирующий множитель существует. Однако, общего метода для его отыскания не существует.
