Будем говорить, что отношение двух функций 
при x 
a есть неопределенность вида 
, если
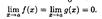
Раскрыть эту неопределенность означает вычислить предел 
, если он существует.Теорема Лопиталя. Пусть функции f(x) и g(х) определены и дифференцируемы в некоторой окрестности точки а за исключением, быть может, самой точки a. Кроме того, пусть 
, причем g'(х) ≠ 0 в указанной окрестности точки а. Тогда если существует предел отношения 
(конечный или бесконечный), то существует и предел 
, причем справедлива формула
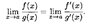Замечание 1. Правило Лопиталя можно применять повторно, если f'(x) и g'(х) удовлетворяют тем же требованиям, что и исходные функции f(x) и g(х).
Замечание 2. Теорема остается верной и в случае, когда х 
(х 
± 
).
