Теорема Ферма (необходимое условие локального экстремума). Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная функции в этой точке равна нулю, т.е. 
Доказательство.
Пусть для определенности 
− точка локального минимума. Тогда 
или 
.Если 
, то 
Если 
, то 
.Таким образом, должны одновременно выполнятся два неравенства:
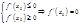. Теорема доказана.
Замечания: 1) Функция 
имеет в точке 
локальный минимум, но 
. 2)Функция 
имеет в точке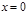 
производную 
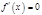, но точка 
не является точкой локального экстремума.
