Пусть 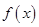 представима интегралом Фурье (т.е.
представима интегралом Фурье (т.е. 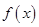 абсолютно интегрируема на
абсолютно интегрируема на 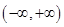 и
и 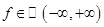 ).
).
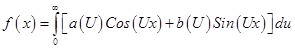 (1)
(1)
Преобразуем выражение стоящее под интегралом, воспользовавшись формулами Эйлера.
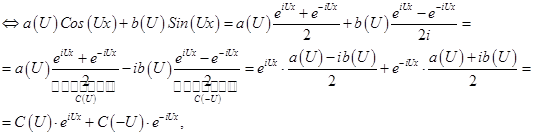
где положено 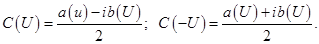
Тогда 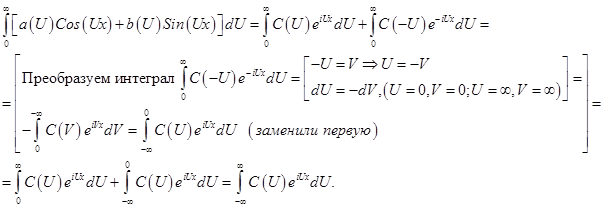
Получим выражение для 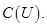
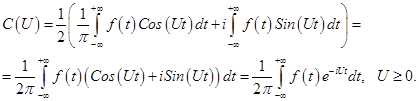
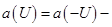 сохраняет свой знак
сохраняет свой знак
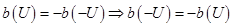 меняет свой знак на противоположный
меняет свой знак на противоположный
Другими словами, 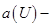 чётная, а
чётная, а 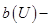 нечётная относительно U.
нечётная относительно U.
(Эти формулы верны и для U<0, т.е. 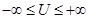 )
)
Итак, в точках дифференцируемости 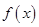 :
:
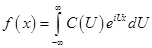 (1), где
(1), где 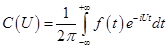 (2).
(2).
Выражение для 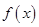 в (1) является комплексной формой интеграла Фурье для функции
в (1) является комплексной формой интеграла Фурье для функции 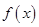 . Если в (1) заменить
. Если в (1) заменить 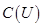 выражением (2), то получим в (…) дифференцируемости функции
выражением (2), то получим в (…) дифференцируемости функции 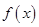 :
:
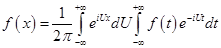 (3) или после внесения под знак внутреннего интеграла
(3) или после внесения под знак внутреннего интеграла 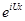 получим:
получим:
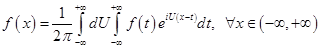 (4).
(4).
Правая часть формулы (4) называется двойным интегралом Фурье в комплексной форме.
На основании представления интеграла Фурье в к.ф. и представления функции чётным и нечётным образом 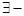 ют преобразования Фурье.
ют преобразования Фурье.