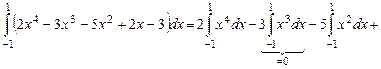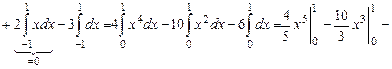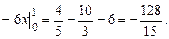Применяя формулу Ньютона – Лейбница, вычислить интегралы:
9.1.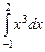 
; 9.2. 
;
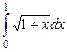9.3.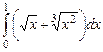 
; 9.4. 
;
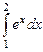9.5.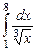 
; 9.6. 
;
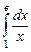9.7.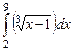 
; 9.8. 
;
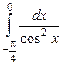9.9.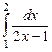 
; 9.10. 
;
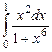9.11.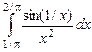 
; 9.12. 
;
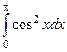9.13.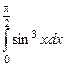 
; 9.14. 
;
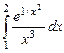9.15.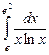 
; 9.16. 
;
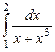9.17.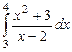 
; 9.18. 
.
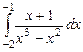При вычислении определенных интегралов полезно обращать внимание на четность интегрируемых функций.
Если функция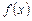 
– нечетна, то интеграл от нее в симметричных пределах равен 0.
Пример.
Вычислить определенный интеграл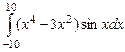 
.
Решение.
Так как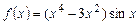 
– нечетная функция, то
.
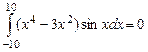Если подынтегральная функция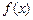 
является четной, то справедливо равенство:
.
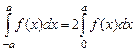Пример.
Вычислить определенный интеграл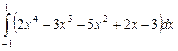 
.
Решение.
