1) 
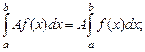
2) 
;
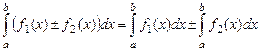4) Если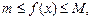 
то 
в частности, если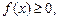 
то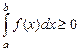 
;
5) Если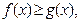 
то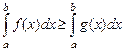 
;
6) Если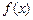 
– непрерывна на 
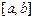, то найдется такая точка 
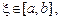что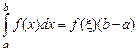 
;
7) 
;
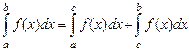
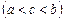8) 
.
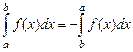Между определенными и неопределенными интегралами существует тесная связь, и эта связь выражается формулой Ньютона – Лейбница
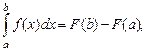(3)
где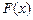 
– некоторая первообразная функции 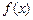. Таким образом, для того, чтобы вычислить определенный интеграл, нужно сначала вычислить неопределенный интеграл, т.е. найти некоторую первообразную функции 
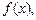а затем воспользоваться формулой (3). Заметим, что при подстановке пределов интегрирования в первообразную, часто пользуются обозначением
.
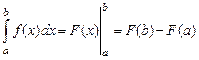Пример.
Вычислить определенный интеграл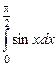 
.
Решение.
.
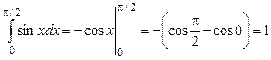