Глава IХ
Определенный интеграл
Определенный интеграл и его свойства
Пусть на отрезке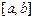 
задана функция 
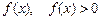. Разобьем этот отрезок на n частей произвольными точками 
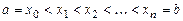(рис.19).
Будем говорить, что этим произведено разбиение R отрезка 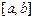. На каждом отрезке 
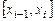выберем произвольную точку 
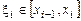и составим сумму
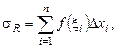(1)
где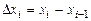 
– длина частичного отрезка. Сумма (1) называется интегральной суммой функции 
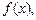соответствующей разбиению R. Геометрически каждое слагаемое 
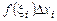представляет собой площадь прямоугольника со сторонам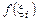и 
и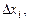 
а вся сумма (1) – есть сумма площадей таких прямоугольников. Эта сумма с некоторой погрешностью выражает площадь фигуры, ограниченной сверху графиком функции 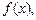снизу – осью абсцисс, а справа и слева прямыми 
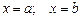. Эта погрешность будет тем меньше, чем “мельче” разбиение R. Если 
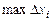устремить к 0, то интегральная сумма (1) дает «в пределе» указанную площадь. Этот предел и будет называться определенным интегралом. Т.е.
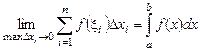, (2)
если:
1) этот предел существует,
2) не зависит от способа разбиения отрезка 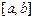на элементарные участки,
3) не зависит от выбора точки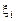 
на каждом участке.
Число a называется нижним пределом интеграла, а число b – верхним его пределом. Функция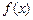 
, для которой существует определенный интеграл (2) называется интегрируемой на отрезке 
