Рассмотрим наиболее простые и распространенные процессы стационарного переноса тепла теплопроводностью. Перенос тепла через плоскую стенку, толщиной

имеющую на внешних поверхностях температуры Исходным является дифференциальное уравнение теплопроводности в виде: и что приводит к следующему решению: где постоянные интегрирования . Определение постоянных приводит к такому решению: выражая: и что имеет смысл полного термического сопротивления в стационарном процессе теплопроводности через плоскую стенку. При многослойной стенке получаем:Здесь сумма: по смыслу есть сумма частных термических сопротивлений в многослойной стенке. Рассмотрим перенос тепла через цилиндрическую стенку. Исходное уравнение имеет вид: Это уравнение для переноса тепла через цилиндрическую стенку с внутренними источниками выделения тепла, плотность которых равна Этого уравнения общее решение имеет следующий вид: где постоянные интегрирования определяются таким образом из следующих граничных условий:

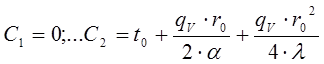В результате получаем следующее решение для распределения температур при переносе тепла теплопроводностью через цилиндрическую стенку с внутренними источниками тепла плотностью и Из этих уравнений получаются формулы и для переноса тепла через

цилиндрическуюстенку без источни и

В итоге и для многослойной цилиндрической стенки получаются формулы близкие по виду к таковым для плоской стенки. Тепловой поток через цилиндрическую поверхность (трубы) можно отнести к единице длины трубы, тогда из полученного выше решения следует:

Здесь: Линейные, отнесенные к единице длины трубы, плотность теплового потока, коэффициент теплопередачи, коэффициент теплопроводности стенки, внутренний и наружный диаметры трубы, коэффициенты теплоотдачи с стороны внутренней и наружной поверхности, температуры на внутренней и наружной поверхностях стенки и температуры потоков, омывающих стенку внутри и снаружи, соответственно. Для линейного коэффициента теплопередачи можно записать:

Тогда для полного термического сопротивления участка трубы длиной в 1м. будем иметь: проводим анализ этой величины на экстремум по внешнему диаметру d2 :Получаем, что есть экстремум по этому параметру. С физической точки зрения он означает наличие максимума линейной плотности теплового потока. Другими словами: есть такое значение внешнего диаметра трубы, при котором линейная плотность теплового потока становится максимальной для данных прочих условий. Это решение характеризует существование так называемого «критического диаметра» трубы. Т.е. если решается задача выбора толщины изоляции, наносимой на внешнюю поверхность трубы, то знание критического позволяет правильно сориентироваться при решении этой задачи. Из анализа структуры приведенных выше формул для коэффициентов теплопередачи следуют важные выводы для практики:

1. В процессе передачи тепла через твердую стенку слагаемое, отвечающее за термическое сопротивление твердой стенки, как правило, вносит меньший вклад в общую сумму, т.е. в многих важных для практики случаях им можно пренебречь. Это означает, что, например, для однослойной стенки трубы можно записать: или Из этой формы записи формулы для коэффициента теплопередачи следует

1.увеличивать интенсивность процесса переноса тепла через некую трубу можно двумя основными путями:1а.увеличивая коэффициенты теплоотдачи;