При численном интегрировании наряду с приближёнными формулами представляет также интерес нахождение нижних и верхних границ интегралов. Рассмотрим два метода оценки интегралов:
а) оценка интеграла в случае когда подинтегральная функция 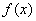 удовлетворяет условию:
удовлетворяет условию:
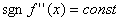 для
для 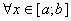 (28)
(28)
б) общий случай.
Рассмотрим интеграл:
 (29)
(29)
где 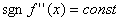
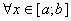 . Не умоляя общность будем считать что
. Не умоляя общность будем считать что 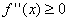
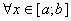 тогда (Рис. 1) ясно что
тогда (Рис. 1) ясно что






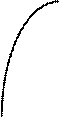

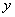
К Е
N
М
0 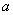
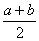
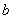
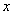
Рис. 1
0 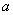
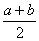
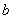
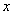
Площадь криволинейной трапеции 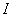 заключена между площадями aMNb и aKEb т.е.
заключена между площадями aMNb и aKEb т.е.
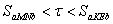 (30)
(30)
Очевидно что
 (31)
(31)
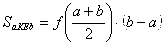 (32)
(32)
Таким образом для оценки интеграла в случае 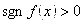 имеем:
имеем:
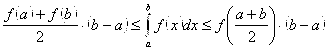 (33)
(33)
если же 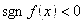 неравенство (33) заменяется на обратное.
неравенство (33) заменяется на обратное.
б) Другой принцип грубой но зато общей оценки значения интеграла основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями 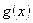 и
и  т.е.
т.е.
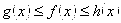
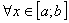 (34)
(34)
Тогда
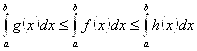 (35)
(35)