Пусть нам нужно вычислить интеграл:
(36)
В случае когда методы Ньютона-Котеса и Гаусса работают плохо приходится обращаться к вероятностным методам случайного поиска. К таким методам относится метод Монте-Карло.
Для вычисления интеграла (36) методом Монте-Карло заменим переменную интегрирования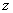 
таким образом чтобы пределы интегрирования 
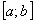отобразились соответственно в 
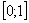. Для этого нужно воспользоваться преобразованием:
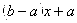(37)
тогда интеграл (36) принимает вид:
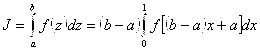(38)
Для вычисления же интеграла на 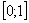имеем формулу:
(39)
где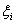 
- случайные числа равномерно распределённые на 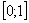. Таким образом по методу Монте-Карло интеграл (36) считается по формуле:
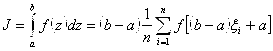(40)
где 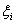- равномерно распределённые случайные числа из промежутка .
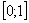Аналогично для кратных интегралов. Получаем:
(41)
где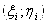 
- случайные точки равномерно распределённые на квадрате 
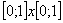(Здесь знак « 
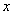» означает декартовое произведение).
В случае когда область интегрирования является сложным множеством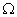 
(рис. 6) пользуемся прямоугольником 
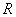который описывается вокруг множества 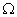. И интеграл по множеству 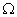заменяем интегралом по прямоугольнику 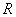который уже умеем вычислять по формуле (41). Замена интеграла по множеству 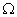производится соотношением:
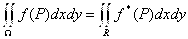(42)
где
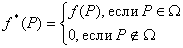(43)
таким образом:
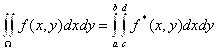(44)
который легко рассчитывается по формуле (41).
Аналогично вычисляются и трёхкратные интегралы. Этот подход легко обобщается для n-кратных интегралов.
