Рассмотрим метод Ньютона-Котеса (т.е.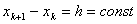 
) в случае интерполяции подинтегральной функции квадратичными функциями на каждом интервале деления. В данном случае мы имеем дело с параболическим интерполированием поэтому на каждом интервале 
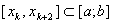необходимо знание значения функции 
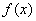в трёх точках (т.к. 
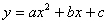имеет 3 неизвестных параметра – коэффициенты 
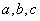). В качестве третьей точки на каждом отрезке 
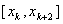- выбирается середина этого отрезка т.е. точка 
.
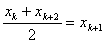Вывод формулы Симпсона будем производить аналитически. Как и в предыдущем случае применяем интерполяционный многочлен Лагранжа для интерполирования функции 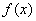на отрезке 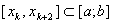при чём считаем что нам известны значения 
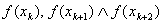. Тогда очевидно что многочлен Лагранжа имеет вид квадратичной функции:
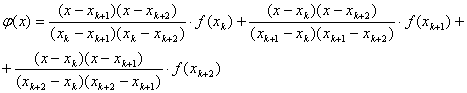(15)
Интегрируя (15) на отрезке 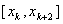будем иметь формулу:
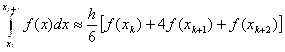(16)
используя свойство аддитивности интеграла получаем:
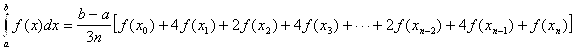(17)
где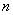 
является четным числом ( 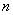- число делений отрезка 
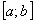т.е. число равных отрезков разбиения).
Формула (17)-называется формулой Симпсона.
Приняв обозначения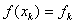 
получаем привычный вид квадратурных формул:
а) Формула трапеций:
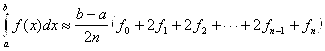(18)
б) Формула парабол (Симпсона) (при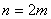 
)
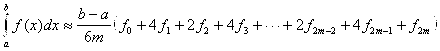(19)
