Частным случаем методов Ньютона-Котеса является квадратурная формула трапеции. Подынтегральную функцию будем интерполировать по формуле Лагранжа в том случае когда на каждом отрезке деления принимается линейная интерполяция а результаты суммируются (рис 1):
Рис. 1.
а) графический вывод:
Определённый интеграл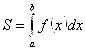 
как известно задаёт площадь 
криволинейной трапеции 
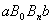поэтому вписав ломаную в дугу кривой 
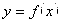мы получаем что площадь криволинейной трапеции можно приближённо вычислить как сумму площадей трапеций:
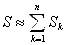(6)
Между тем очевидно что
(7)
Так как в методах Ньютона-Котеса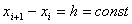 
учитывая (6) получаем:
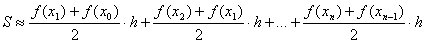(8)
или соединяя подобные члены имеем:
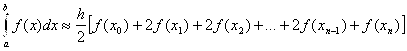(9)
Формула (9) – называется формулой трапеций.
б) Аналитический вывод:
Выведем формулу трапеции аналитическим способом. Для этого используем интерполяционный многочлен Лагранжа для отрезка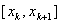 
построим многочлен первой степени который на концах отрезка принимает заданные значения 
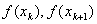. Ясно что в таком случае интерполирующая функция 
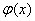имеет вид:
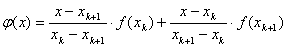(10)
т.к. в методе Ньютона-Котеса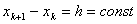 
учитывая (3) и (4) из (10) получаем:
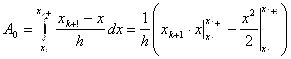
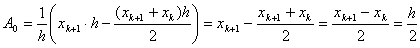(11)
Аналогично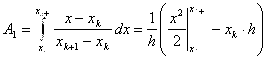 
т.е.
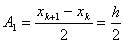(12)
Таким образом получаем формулу:
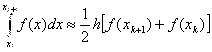(13)
тогда используя свойство аддитивности оператора интегрирования имеем:
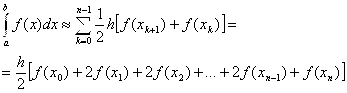(14)
где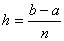 
. Получили формулу (14) трапеций которая естественно совпадает с (9).
