Реферат
ПО МАТЕМАТИКЕ
На тему
“Способы вычисления интегралов”
Выполнил: студент гр.2С1
Ботвиньев В.А.
Проверила: преподаватель
Шебекино
2014-2015
Численные методы вычисления интегралов. Метод Ньютона-Котеса. Метод Гаусса
Численные методы вычисления интегралов. Постановка задачи
Решая физические задачи часто приходится вычислять значения определённых интегралов от функций 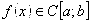 . Во многих случаях в виду того что подлежащий вычислению интеграл не выражается через элементарные функции прибегают к приближённым численным методам.
. Во многих случаях в виду того что подлежащий вычислению интеграл не выражается через элементарные функции прибегают к приближённым численным методам.
Прежде всего рассмотрим случай когда 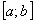 - конечный интервал.
- конечный интервал.
В таком случае как известно функция 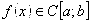 является ограниченной т.е.
является ограниченной т.е. 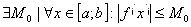 . В этом случае наиболее часто применяемый численный метод интегрирования состоит в том что интеграл от
. В этом случае наиболее часто применяемый численный метод интегрирования состоит в том что интеграл от 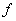 заменяется некоторой линейной комбинацией значений
заменяется некоторой линейной комбинацией значений  в
в 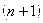 точках
точках 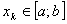 :
:
 (1)
(1)
Формула (1) называется квадратурной формулой а коэффициенты 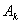 - квадратурными коэффициентами или весами абсциссы
- квадратурными коэффициентами или весами абсциссы 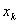 - узлами квадратурной формулы.
- узлами квадратурной формулы.
Методы численного интегрирования классифицируются в зависимости от того заданы ли значения аргумента через равные промежутки или нет. Так методы Ньютона-Котеса требуют чтобы значения 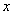 были заданы с постоянным шагом а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов.
были заданы с постоянным шагом а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов.