На каждом шаге любого состояния системы решение нужно выбирать «с оглядкой», но на последнем шаге - локально-оптимальным.
Z 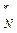 (S
(S  ) = max f
) = max f 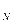 (S
(S  , X
, X 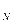 ) – условный максимум на n-шаге
) – условный максимум на n-шаге
X 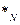 ( S
( S  ) – условное оптимальное управление
) – условное оптимальное управление
Z 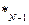 (S
(S  ) = max
) = max  ( S
( S 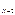 , X
, X 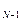
 ) + Z
) + Z 
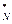 (S
(S  )
) 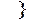


Z 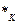 (S
(S 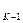 ) = max
) = max 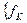 (S
(S 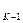 , X
, X 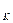 ) + Z
) + Z  (S
(S 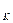 )
) 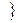 - уравнения Беллмана
- уравнения Беллмана
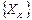
Процесс решения этих уравнений называется условной оптимизацией, результатом которой являются:
Z 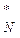 (S
(S  ), …………………Z
), …………………Z  (S
(S 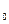 ) и
) и
X 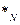 ( S
( S  ),……………X
),……………X  (S
(S 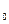 )
)
Далее нужно провести безусловную оптимизацию:
Z 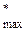 = Z
= Z  (S
(S 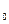 ), X
), X  = X
= X  (S
(S 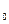 ) и S
) и S  =
= 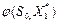 и т.д., подставляя в последовательность условных оптимальных управлений. Получаем оптимальное решение задачи- X
и т.д., подставляя в последовательность условных оптимальных управлений. Получаем оптимальное решение задачи- X 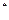 = (X
= (X 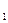 , …..X
, …..X  ).
).