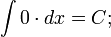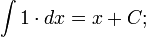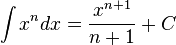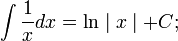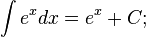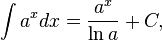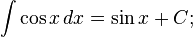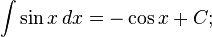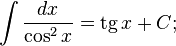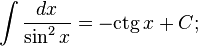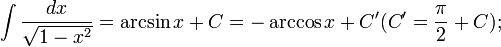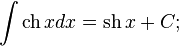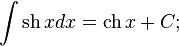Выражение вида 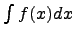 называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом
называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом 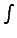 всегда присутствует dx.
всегда присутствует dx.
Определение. Неопределенным интегралом 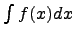 называется функция F(x)+C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е.
называется функция F(x)+C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е.
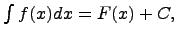 . Функцию F(x) называют первообразной функции f(x). Первообразная функции f(x) определяется с точностью до постоянной величины.
. Функцию F(x) называют первообразной функции f(x). Первообразная функции f(x) определяется с точностью до постоянной величины.
dF(x) - дифференциал функции F(x) и определяется следующим образом:
 Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.
Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.
Замена по частям Для вычисления интеграла 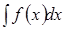 сделаем замену
сделаем замену 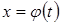 , где
, где 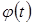 выбирается так, чтобы после преобразований данного интеграла и новой переменной t, получился интеграл, который берется непосредственно.
выбирается так, чтобы после преобразований данного интеграла и новой переменной t, получился интеграл, который берется непосредственно.
Предварительно находим 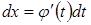 , тогда
, тогда 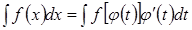 После нахождения первообразной F(t) необходимо вернуться к первоначальной переменной «х».
После нахождения первообразной F(t) необходимо вернуться к первоначальной переменной «х».
Пример
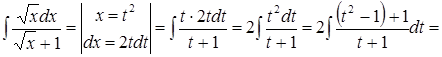
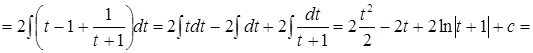
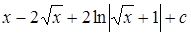
Свойства неопределенного интеграла:
1. 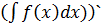 =f(x)
=f(x)
2. 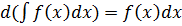
3. 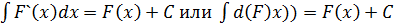
4. 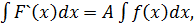 A
A 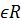
5. 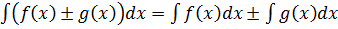
Таблица основных интегралов: