Рассмотрим интеграл от функций cos(x) и sin(x)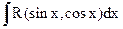 
1) универсальная подстановка
- универсальная подстановка
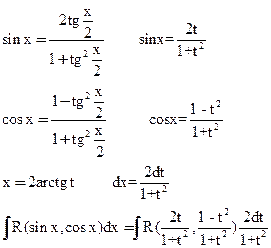
- интеграл от рациональной функции
2)
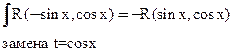
3)
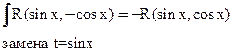
4)
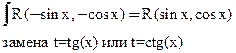
Пример
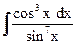
1) Универсальная тригонометрическая подстановка
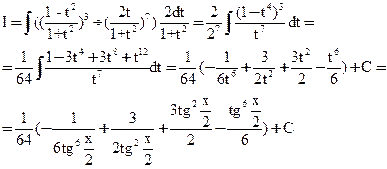
2)
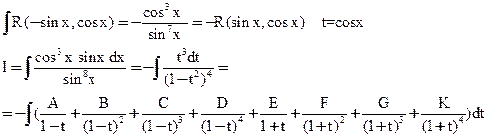
3)
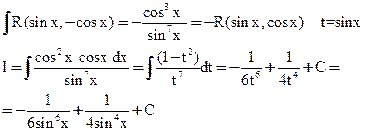
4)
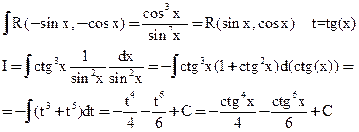
Кроме вышеуказанных подстановок полезно использовать тригонометрические формулы.
Пример
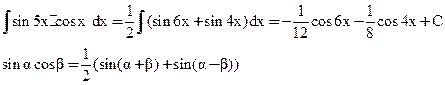
Пример
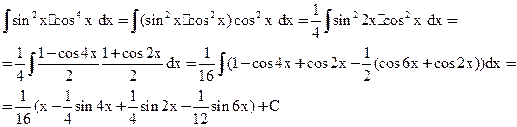
Пример
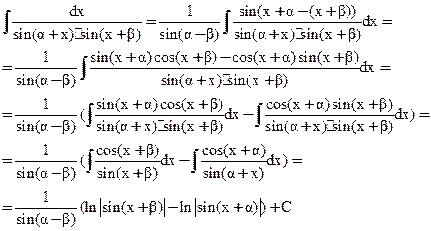
Не все интегралы выражаются в элементарных функциях. Те интегралы, которые нельзя выразить, называются не берущимися.
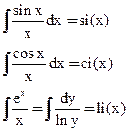
- синус интегральный
- косинус интегральный
- интегральный логарифм
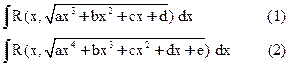
Интегралы (1) и (2) называются эллиптическими
(1) сводится к (2) . Любой кубический многочлен с действительными коэффициентами имеет хотя бы один действительный корень.
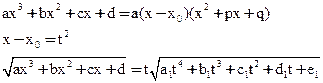
После некоторых преобразований вычисление (2) сводится к вычислению трёх интегралов
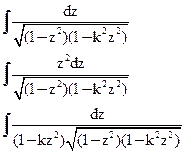- эллиптические интегралы 1-го 2-го и 3-го рода
Упрощение Лежандра
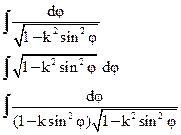
- эллиптические интегралы 1-го 2-го и 3-го рода
в форме Лежандра
Для последних интегралов составлены таблицы
